1. 19.6 鲍姆-韦尔奇算法简介

1.1. 学习目标

• 了解鲍姆-韦尔奇算法

1.2. 1 鲍姆-韦尔奇算法简介

模型参数学习问题 —— 鲍姆-韦尔奇（Baum-Welch）算法(状态未知) ，

• 即给定观测序列，估计模型的λ=(A,B,Π)参数，使该模型下观测序列的条件概率最P(O|λ)大。
• 它的解法最常用的是鲍姆-韦尔奇算法，其实就是基于EM算法的求解，只不过鲍姆-韦尔奇算法出现的时代，EM算法还没有被抽象出来，所以被叫为鲍姆-韦尔奇算法。

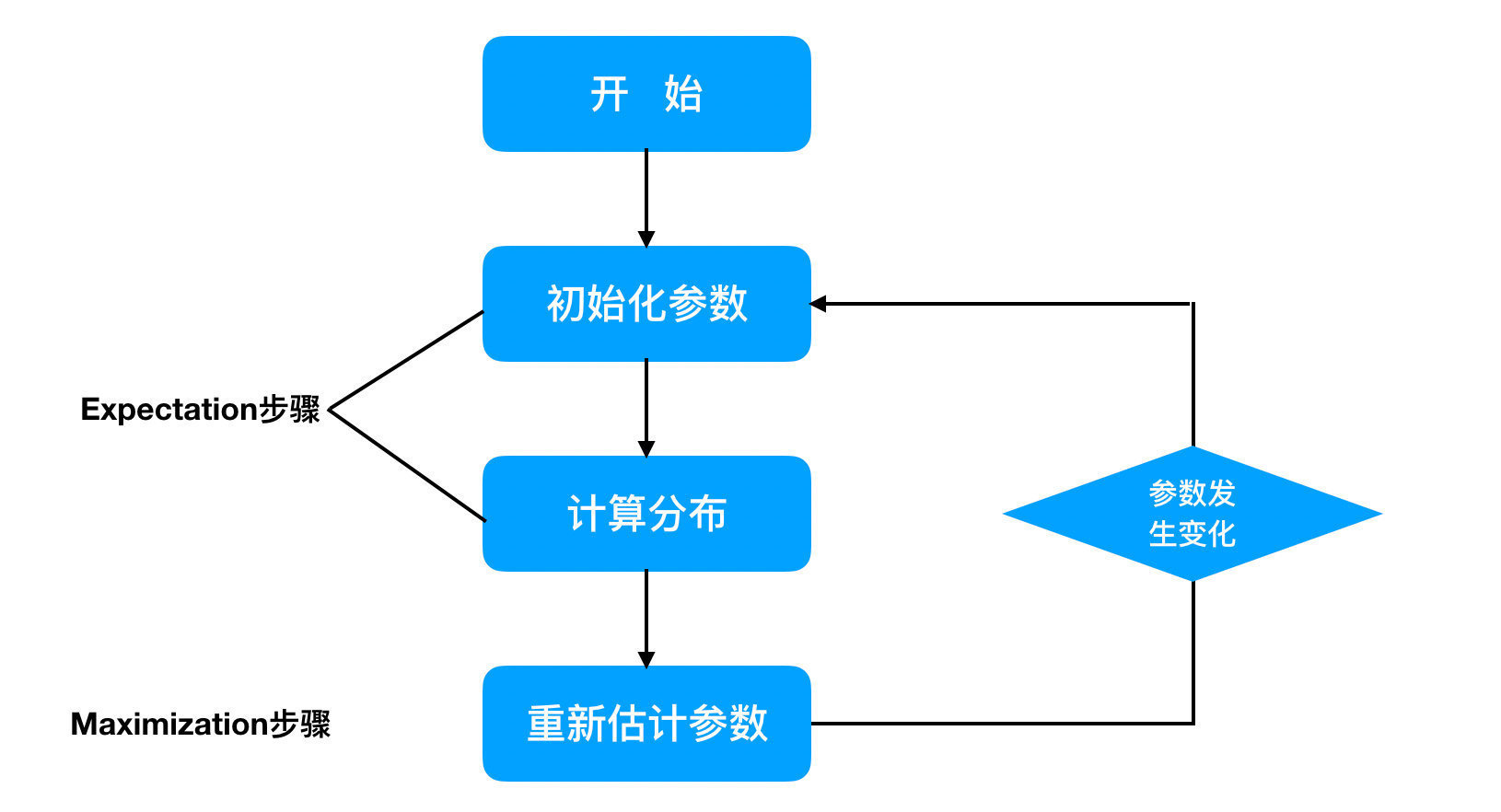
1.3. 2 鲍姆-韦尔奇算法原理

鲍姆-韦尔奇算法原理既然使用的就是EM算法的原理，

• 那么我们需要在E步求出联合分布P(O,I|λ)基于条件概率的期望，其中为当前的模型参数，
• 然后在M步最大化这个期望，得到更新的模型参数λ。

接着不停的进行EM迭代，直到模型参数的值收敛为止。

首先来看看E步，当前模型参数为, 联合分布P(O,I|λ)基于条件概率的期望表达式为：

• $L(\lambda, \overline{\lambda}) = \sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda)$

在M步，我们极大化上式，然后得到更新后的模型参数如下：　

• $\overline{\lambda} = arg\;\max_{\lambda}\sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda)$

通过不断的E步和M步的迭代，直到收敛。